TEMA 5
TEMA 5: ESTADÍSTICOS UNIVARIABLES: MEDIDAS RESUMEN PARA VARIABLES CUANTITATIVAS
Además de las tablas explicadas en el tema anterior, también existen las estadísticas para poner en evidencia los datos observados. Hay tres grupos de medida estadística:
- Medidas de tendencia central: Crean tendencia de valores al resto de datos. Media, mediana y moda.
- Medidas de posición: Formación de grupos ordenados con la misma cantidad de individuos. Cuartiles, deciles y percentiles.
- Mediadas de dispersión o variabilidad: Informan de la variabilidad de las observaciones. Rango, desviación media, varianza, desviación típica y coeficiente de variación.
MEDIDAS DE TENDENCIA CENTRAL
- MEDIA: Es el centro de los datos. La más utilizada en estadística descriptiva.
La suma de las desviaciones respecto a la media = 0
La media NO se altera por una transformación lineal de escala (por una constante)
Alta sensibilidad a puntuaciones extremas
También puede ser media aritmética (descrita anteriormente), geométrica, armónica y aritmética ponderada
- MEDIANA: Puntuación central entre todos los datos. Para ello, es necesario un orden. Se debe calcular siempre que haya pocos datos o estén truncados.
Si es par, la
mediana será la media entre los valores n/2 y (n/2)+1
Si coincide con la media, la distribución de la variable es simétrica
Poca sensibilidad a puntuaciones extremas
- MODA: Es el valor más repetido. Dependiendo del número de modas, puede ser unimodal, bimodal o multimodal. Es la medida menos empleada.
En una distribución unimodal simétrica: media = mediana = moda
MEDIDAS DE POSICIÓN
- CUANTILES: El cuantil 'n' es el valor de la variable y por debajo se encuentra una frecuencia acumulada n. Pueden ser percentiles (100), deciles (10) y cuartiles (4), según dividan la muestra.
- DECILES: La muestra en 10 partes (10%). Son 9 valores que dividen la distribución. El decil “i” (Di), es aquél valor que, ordenadas las
observaciones en forma creciente, el i/10% de ellas son
menores que él y el (100-i)/10% restante son mayores. D5 = P50 = mediana.
- CUARTILES: La muestra en 4 partes (25%). Son 3 valores que dividen la distribución. Q2 = D5 = P50 = mediana
MEDIDAS DE DISPERSIÓN
Resuelve la limitación de las medidas de tendencia.
- RANGO O RECORRIDO (R): Se toma la puntuación mayor y se resta la menor. Limitación: Condicionado a valores extremos.
- RECORRIDO SEMIINTERCUARTÍLICO: Mitad del recorrido intercuartílico. Da mayor estabilidad que el rango al utilizar valores intermedios.
- DESVIACIÓN MEDIA: Es la media de las distancias de cada valor con respecto a la media de la muestra.
- VARIANZA: Es la media de los cuadrados de las diferencias entre cada valor de la variable y la media aritmética de la distribución. Cuanto más pequeña sea, menor será la dispersión.
- DESVIACIÓN TÍPICA: La más utilizada en estadística descriptiva. Es la dispersión de la distribución. Si a todos los valores se les suma la desviación, no varían, pero si se multiplican, la desviación también queda multiplicada. Es sensible a puntuaciones extremas. Si no se puede hallar la media, tampoco la desviación típica. Cuanto más pequeña, mayor concentración de valores alrededor de la media.
- COEFICIENTE DE VARIACIÓN (CV): Se divide la desviación típica entre la media, expresándose en %. No debe usarse cuando la variable presenta valores negativos o 0.
DISTRIBUCIÓN NORMAL O DE GAUSS
Es la que aparece con más frecuencia. Tiene forma de campana y es simétrica respecto al centro.
MEDIDAS DE FORMA
Las medidas de forma indican la simetría de la curva y grado de apuntamiento.
- ASIMÉTRICA: Las medidas de forma indican la simetría de la curva y grado de apuntamiento. Las asimétricas o sesgadas se caracterizan por tener el pico descentrado, adoptando valores entre -1 y 1. (g1 = cola de distribución)
- g1 > 0 → Distribución asimétrica positiva, hacia la izquierda
- g1 < 0 → Distribución asimétrica negativa, hacia la derecha
- CURTOSIS O APUNTAMIENTO: Mide el grado de concentración de valores en torno a la media. Valores entre -1 y 1. En una distribución normal, sería 0. (g2 = curtosis)
- g2 > 0 → Distribución leptocúrtica
- g2 < 0 → Distribución platicúrtica

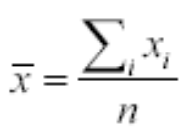

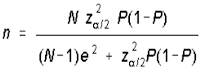
Comentarios
Publicar un comentario